Kinectic Isotope Effects

动力学同位素效应KIE

Kinectic Isotope Effects

动力学同位素效应
Kinectic Isotope Effects(KIE)
动力学同位素效应 (KIE) 是由分子中给定同位素的变化引起的反应速率变化。这是由质量差异引起的，影响振动频率和/或隧穿概率。
当可以被同位素取代的原子发生键断裂或形成时，经常利用这种效应来研究反应机制。这些 KIE 在某种程度上是可预测的，具体取决于质量比，因此可用于验证提出的机制。
我们还可以使用 ORCA 对 KIE 进行量子力学预测，并使用这些预测进一步研究化学反应性。

通过羟基自由基来预测甲烷的 H 原子提取中的 KIE，这是在气相中以高精度测量的

KIE in a H-atom abstraction

为了预测KIE，必须首先寻找反应的过渡态。

1
2
3

!B3LYP DEF2-SVP D3 OPT FREQ
%FREQ   TEMP    293     END
* xyzFILE 0 2 reactants.xyz

1
2
3

!B3LYP DEF2-SVP D3 OPT FREQ
%FREQ   TEMP    293     END
* xyzFILE 0 2 products.xyz

NEB-TS计算

!B3LYP DEF2-SVP D3 FREQ ZOOM-NEB-TS
%FREQ   TEMP    293     END
%NEB    NEB_END_XYZFILE "products_optimized.xyz" END
* xyzFile 0 2 reactants_optimized.xyz

这是一个棘手的案例，无论多小的体系，为了帮助优化，我们使用ZOOM-NEB-TS方法

结果分析

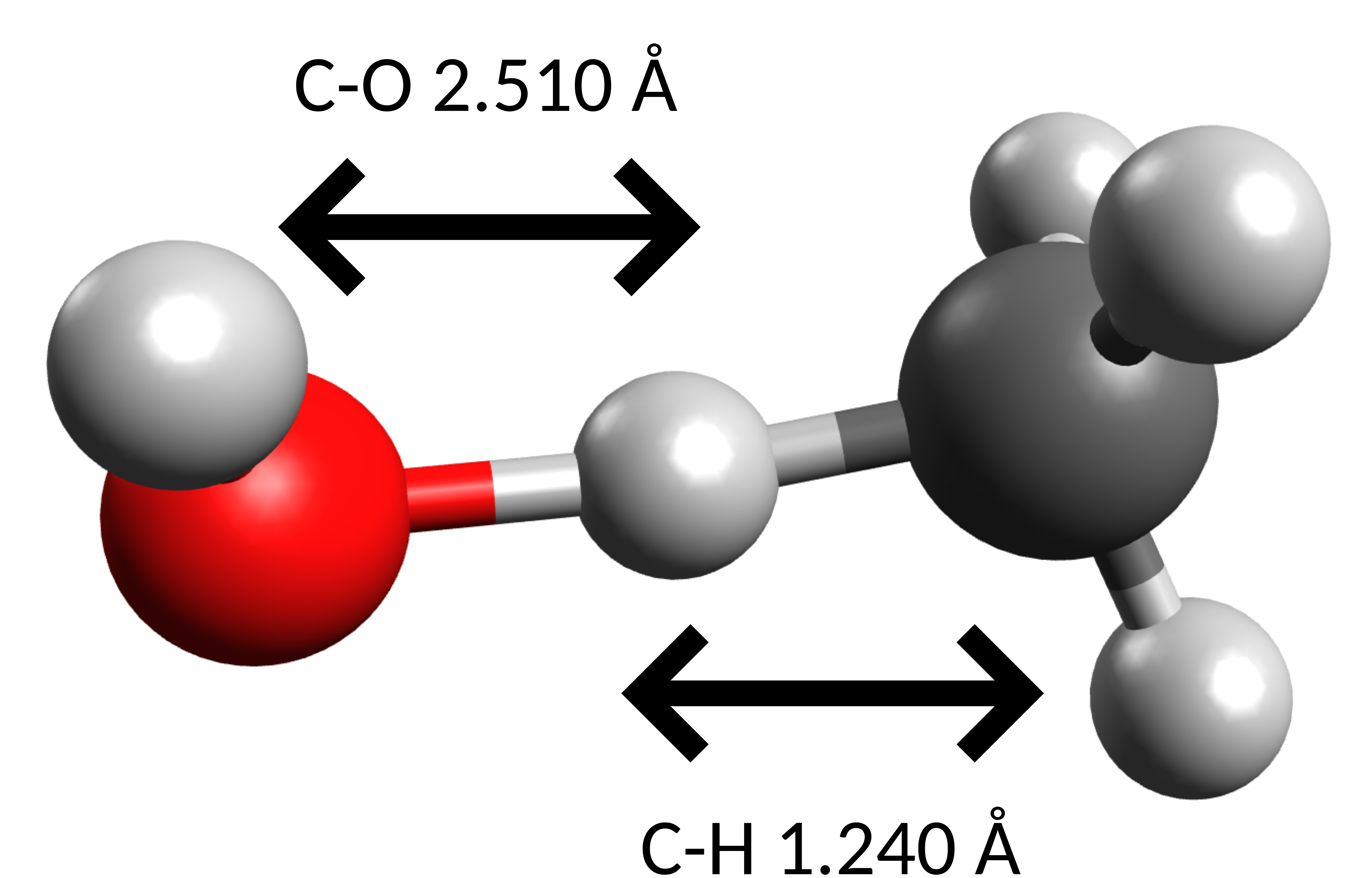
which is the rather obvious pathway for an H-atom abstraction, and presents a single negative frequency of −1070cm⁻¹ along the O-H-C coordinate.
Using the previously explained method in the Thermodynamics and Calculating accurate energy barriers sections, the ΔG^‡_H calculated is 10.11 kJmol⁻¹。

改变同位素

Now, we need to compute the ΔG‡ for the reaction involving the deuterated methane. Assuming that the bond lengths and electronic energies are the same, which is very well true for such a small change in the mass, one needs only to recompute the vibrational corrections to the Gibbs free energy.

That can be easily done using the !PRINTTHERMOCHEM flag, also already presented in the Thermodynamics section, without the need to repeat the whole optimization plus NEB-TS process.

In this case, we only need to add the mass of the new isotope on the geometry section of the input, such as:

!PRINTTHERMOCHEM
%GEOM   INHESSNAME      "R.hess"   END
%FREQ   TEMP    293   END
* xyz 0 2
  C     -2.411352    1.128722    0.029849
  H     -1.342943    1.352019   -0.097229 M 2.00141
  H     -2.853386    0.899279   -0.950538 M 2.00141
  H     -2.919524    2.002716    0.462768 M 2.00141
  H     -2.541362    0.264118    0.697923 M 2.00141
  O      1.133678    1.702618    0.011070
  H      0.792228    1.085478    0.693266
*

for both the reactant and the TS. The M 2.00141 after the coordinates of the hydrogens indicate that these atoms now should have the mass of 2.00141amu, corresponding to a deuterium atom. Of course, this is atom-specific and the hydroxyl radical stays the same.

Now, a new correction to transform the electronic energy into G^o is printed, and the new ΔG^‡_D can be obtained, with a value of 14.90 kJmol⁻¹.

Calculating the KIE

KIE与系统的零点能量Zero Point Energy(ZPE)有关，当振动频率由于质量改变而降低或减少时，ZPE会变化
在示例中，较重的氘会降低频率，从而降低ZPE并改变能垒
反应物ZPE比过渡态更容易受影响，因为它结合力更强，吉布斯自由能的变化也不均匀
With the new barriers, come the new rates and the KIE is then computed as the ratio of kH/kD, that in terms of free energies is given by:
$$
\frac{k_H}{k_D}=e^{\frac{-\Delta G_H - \delta G_D}{RT}}
$$
Using both free energy barriers calculated, this ratio is predicted to be 7.41, well within the experimental value of 6.75±0.83. That is a high value for a primary isotope effect, but in this case it makes sense if one considers that the transition state is directly dependent on the bonds with the hydrogen atom.

结构

#Reactant
C     -2.42007     1.14475     0.00503
H     -1.37176     1.42602    -0.24888
H     -2.95035     0.87504    -0.97240
H     -2.97696     2.02414     0.50780
H     -2.39461     0.26127     0.72431
O      1.11295     1.79481    -0.12688
H      0.85814     0.90892     0.95813

#Product
C     -2.640806    0.931381    0.002030
H      0.593417    1.397564   -0.537054
H     -3.426646    1.364904   -0.619289
H     -1.670863    1.425720    0.075351
H     -2.839810    0.009183    0.550600
O      0.590809    2.120231    0.105838
H      0.558140    1.654177    0.952824