预测NMR核磁光谱
NMR光谱
ORCA能够被用来预测NMR光谱 ORCA can also be used to predict NMR spectra, both in the form of NMR shifts for any nucleus and J couplings for any pair of nuclei. Here we will discuss both cases, exemplifying with an organic acid and toluene.
C-NMR spectra of the propionic acid
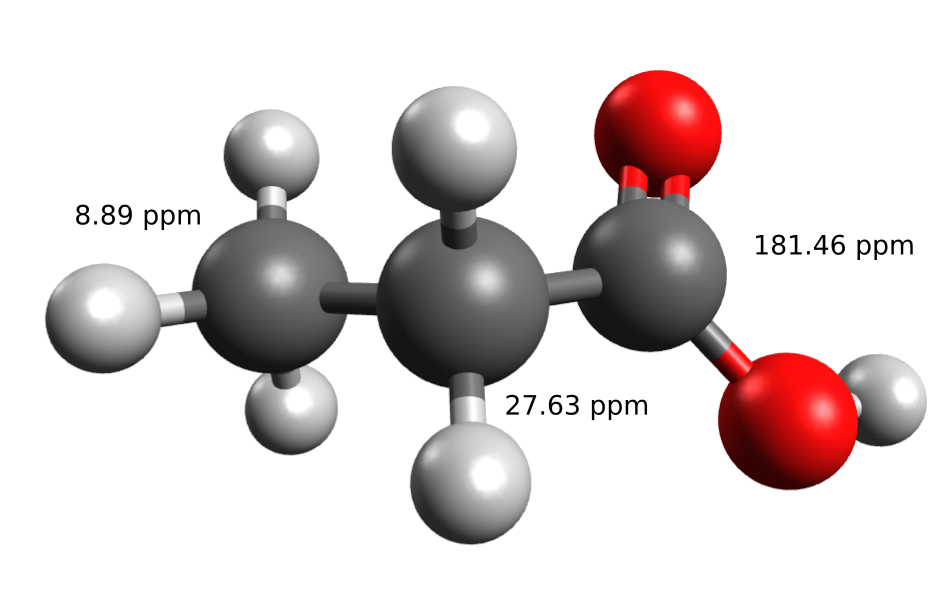
丙酸的NMR谱 计算氯仿中丙酸的C-NMR位移,其实验数据能在SDBS数据库中找到
几何优化
1 | !B3LYP DEF2-TZVPP D3 OPT |
Always have in mind that NMR shifts are quite dependent on the conformer you choose. A conformer search or even a Boltzmann weighting might be necessary!
Having your structure optimized, the NMR shieldings are requested by
adding NMR on the first input line and adding the specifics under the
%EPRNMR block, that should always come
after the geometry section. To request the NMR
shieldings, just add {SHIFT} after the atom assignments:
1 | !B3LYP DEF2-TZVPP NMR |
The default algorithm uses Gauge-Independent Atomic Orbitals (GIAO, This is quite important in NMR calculations and we do not recommended turning this off unless you really know what you are doing.
If one just types NMR on the first line, without specifying the nuclei below, then shieldings for all the atoms will calculated. Specific atoms can be added as a list, following what is described in Predicting EPR.
After a successful SCF calculation, the output starts with the heading:
1 | ------------------------------------------------------------------------------ |
Now, you can see some details of the calculation, with the GIAO as the Treatment of gauge, and the number of nuclei that will be covered. Then the GIAO integrals are solved:
1 | One-electron GIAO integrals (SHARK) ... done |
followed by the CP-SCF calculations necessary to derivatives and finally the chemical shieldings are computed:
1 | --------------- |
First, you can see that the results for carbon number 0 are printed (0C), with all its specific contributions, and the other atoms requested follow in order. Usually, the number that we actually measure is related to the isotropic shift, that is printed after iso=.
Chemically equivalent nuclei might have slight different shieldings, due to geometric asymmetries. In that case, the best thing to do is just average them.
At the end of the file, a summary is printed, with the isotropic part and the anisotropy:
1 | -------------------------------- |
These NMR shieldings are not comparable the experimental ones! One still needs to compute a reference shielding or use an internal standard to convert to proper experimental shifts. Please read the next sections on how to do that.
Calculating the reference NMR shieldings
Similarly to the experiment, the absolute values of the shieldings have no much meaning without a reference value, and we might need to compute those as well. In the case of 13C-NMR and 1H-NMR, you can use TMS (Tetramethylsilane), which is also the usual experimental reference for that. Just optimize and compute the C-NMR of TMS by running the input such as:
1 | !B3LYP DEF2-TZVPP NMR |
1 | -------------------------------- |
Now, the average value of the C-NMR shieldings can be used to compute the shifts that are comparable to the experimental by using: \[ \sigma_{calc}=\sigma_{ref}-\sigma_{targethmol} \] and the results for three different calculation levels, using the B3LYP-optimized structures, are:
| Method | δ1δ1 | δ2δ2 | δ3δ3 |
|---|---|---|---|
| HF-RIJCOSX | 10.5 | 27.1 | 184.1 |
| BP | 9.8 | 29.0 | 176.8 |
| B3LYP | 10.2 | 29.2 | 181.2 |
| Exp. | 8.9 | 27.6 | 181.5 |
Have in mind that the refence should always use the same level of theory as the target molecule, including any solvation effects or approximations such as the RI.
The use of an internal standard
Instead of calculating a reference molecule, you can also just apply a constant shift to the calculated peaks, so that one of them is equal to a know value.
One could use the value of an assigned methyl or an aromatic H or C and benefit from possible error cancellations. This also makes more sense if the reference is too different from the target molecule or it is somehow complicated to simulate, like phosphoric acid for 31P-NMR.
H-NMR of toluene and J couplings
The same scheme can be used to predict the H-NMR and the couplings.
Let's do it for toluene, for which the reference values can also be
found at SDBS.
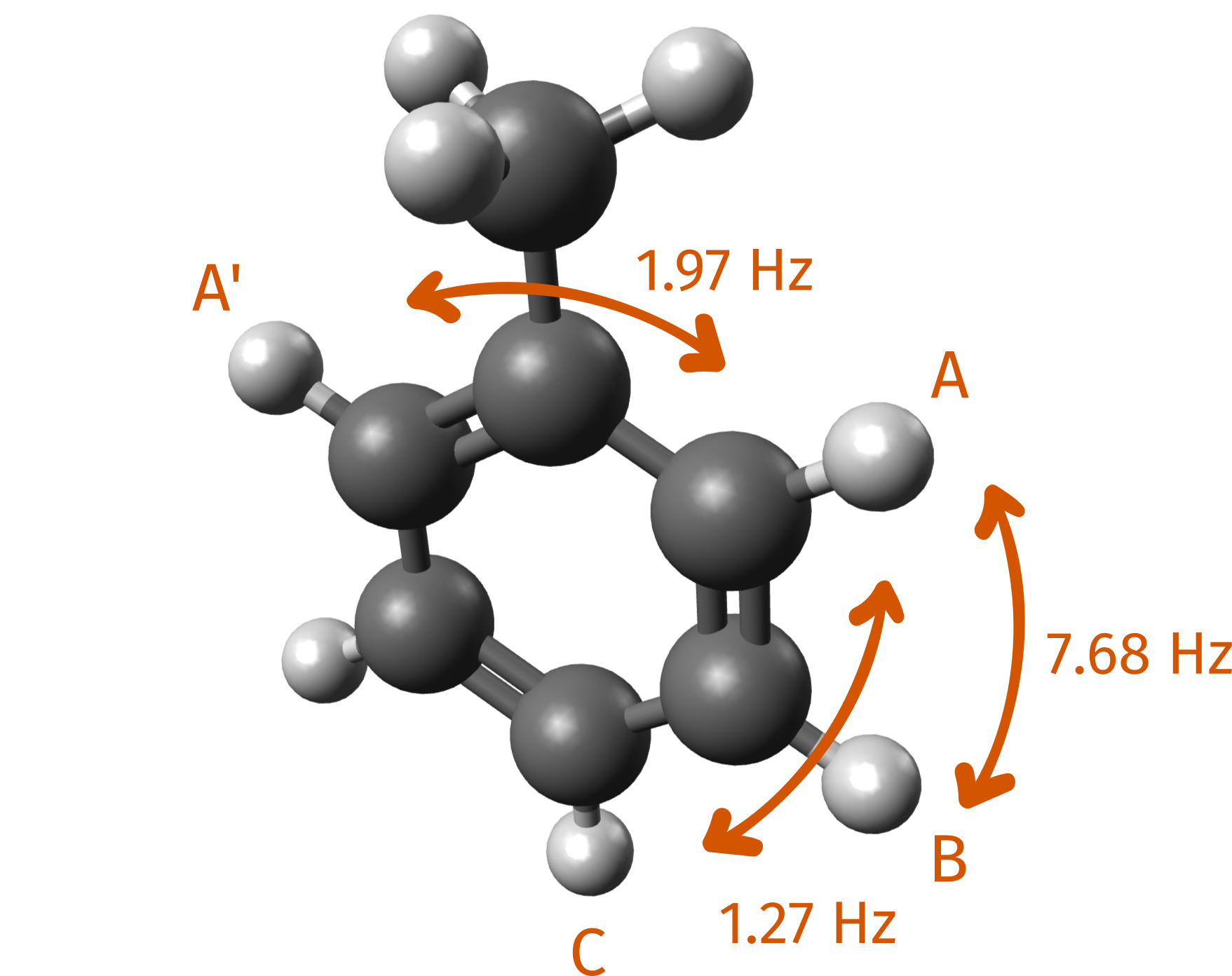
Here we highlight some of the J couplings between hydrogen atoms, as
labeled on the database:
Again, first we optimize the structure and then compute the shieldings. This time, we will use one of the Implicit Solvation Models to include the effect of chloroform:
1 | !B3LYP PCSSEG-2 AUTOAUX NMR CPCM(CHLOROFORM) |
Here we used the pcSseg-2 basis, which is well suited for NMR calculations, and the AUTOAUX flag was chosen to automatically build the necessary auxiliary basis.
After the output that was already discussed, the coupling section is printed:
1 | NMR SPIN-SPIN COUPLING CONSTANTS |
Since we used the SSALL option, all components of the coupling are included. For the specifics on how to turn these on and off, please check the ORCA manual (must log in).
Then comes a detailed description of these couplings, starting from one atom and listing closest neighbors (there is a cutoff radius of 55 Å):
1 | ================================ |
all couplings are listed, in Hz, as:
1 | ----------------------------------------------------------- |
Once more, the value that correspond to what most experiment measures comes after the iso=
The values are printed in Hz, so in order to convert them to ppm one has to take into account the equipment's frequency. In our case, the database says it was measured in 300 MHz NMR, so that the coupling in ppm would be: \[ J_ppm=J_{Hz/{\omega_{equip}MHZ}}=J_{Hz}/300 \]
A summary of the results is given below
| Coupling | Calculated (ppm, Hz) | Experiment (ppm, Hz) |
|---|---|---|
| A - A' | 0.006, 1.88 | 0.007, 1.97 |
| A - B | 0.022, 6.68 | 0.026, 7.68 |
| A - C | 0.004, 1.16 | 0.004, 1.27 |
NMR prediction using double-hybrids
In ORCA, the NMR properties can also be computed using the
double-hybrid functionals, that profit from adding MP2 correlation to
DFT . These can be used by setting the NOFROZENCORE flag,
together with the desired functional:
1 | !RI-B2PLYP PCSSEG-3 AUTOAUX NMR |
In that case the NMR calculation runs twice. First, ORCA does only the DFT part
1 | ***************************************** |
and, at the end, the analytic MP2 derivatives are computed:
1 | Calculating analytic MP2 second derivatives ... (>DSD-TOL_H.last_mp2_re) done |
That can take some time, while no other message will be printed. After finishing these derivatives, the MP2 part is added and the results are printed under the header:
1 | ************************************** |
In our experience, there provide the most reliable results at a cheaper level of theory and can be used even together with spin-scaled double-hybrids such as the RI-DSD-PBEP86.
TIPs
- The pcSseg-2 is recommended for HF/DFT and pcSseg-3 for MP2/double-hybrids.
- TPSS, TPSSh or DSD-PBEP86 D3BJ are in general the best methods.
Structures
1 | # 1-propionic acid |